The Use of Phase Comparators in Frequency Measurement

 

by David Archer

 

Introduction

 

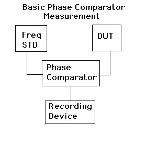Phase comparators are devices that measure the accumulated phase difference between a reference frequency standard and a frequency standard that is being characterized. The advantage of such of a device is that it can be used to continuously compare two frequency standards.

 

Typically these are connected to something like a strip chart recorder or to some sort of monitoring device so that the accumulated phase can recorded over a period of time.

 

This paper will cover the basic use of phase comparators in frequency standard characterization.

 

Background

 

A metric that characterizes the difference between a frequency standard from a nominal frequency is called the fractional frequency deviation. The fractional frequency deviation is defined as

 

           

 

where f is the frequency of the standard, and f₀ is the nominal frequency. This ratio is usually expressed in parts, for instance a good crystal oscillator might have a specification of 1 part in 10⁸ over some timescale.

 

A sinusoidal waveform x(t) is of the form

 

           

 

where F(t) is called the phase of the sinusoid. A sinusoid of frequency f₀ has a phase of the form

 

           

 

One can define the instantaneous frequency by

 

           

 

In the case where the frequency can be a function of time, deviating from the nominal frequency, one can write the phase as

 

           

 

From this it follows that the fractional frequency deviation at time t can be found from:

 

 

If the accumulated phase over a time Δt is Δφ the average fractional frequency difference between the standard and the frequency standard being tested over that time interval is:

 

 

and the average frequency of the DUT is

 

 

It should be noted that all the phases here are measured in radians. To convert these formulas into ones involving phase in degrees, replace 2π by 360 wherever it occurs.

 

Uncertainty

 

This analysis starts with the expression for the DUT frequency when the phase comparator measures phase in degrees

 

           

 

Assuming for the moment that the long-term uncertainty of the frequency of the standard expected over the time interval of the measurement is δf0, the phase measurement uncertainty is δφ, and the uncertainty of the time interval of the recording device is δt; one can determine that the worst-case uncertainty of the frequency of the DUT is

 

           

 

Notice that one can never do any better than the uncertainty of the frequency standard, as expected; but the last two terms decrease in time. This indicates that if one waits long enough, the uncertainty approaches that of the standard. This is not exactly true, as the uncertainty of the standard will in general not be constant over time, and there are other assumptions made here that are not valid over all time scales. This is reasonably accurate though over most lab time scales.

 

Looking at this equation another way, it tells how long one has to measure the accumulated phase change in order to keep the measurement at a certain level of uncertainty.

 

The uncertainty in the fractional frequency deviation is just

 

.

 

Since y is a direct measure of the uncertainty in the DUT, one can define the TUR of the measurement as

 

            .

 

Assuming one has an accurate enough frequency standard where a 4:1 TUR is possible, this TUR can only be achieved if the measurement time Δt is long enough such that

 

           

 

The accumulated phase shift is maximum when

 

           

 

Substituting this into the previous equation and one obtains for the minimum time to maintain a 4:1 TUR

 

           

 

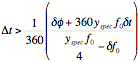
This equation is only valid if

 

            ,

 

that is the standard must be greater than 4 times better than the spec one is trying to verify.

Conclusion

 

The basic use of phase comparators has been described, along with a basic uncertainty analysis. The minimum time required to record data in order to meet a 4:1 TUR in the measurement was also derived, assuming that the frequency standard is sufficiently accurate.

 

The phase comparator is still in use in many standards labs for the comparison of frequency, although it is older technology. For long-term monitoring of frequency standards it is very useful.