Power Splitter Equivalent Reflection Coefficient Sensitivity Analysis
Abstract
Often power calibrations are performed using a power splitter in a leveling configuration to provide a stable available power to compare a standard power measurement device with an unknown. From this configuration one can establish the equivalent source reflection coefficient through the scattering parameters of the power splitter. To perform an uncertainty analysis of this type of power calibration one needs to determine the uncertainty associated of the source reflection coefficient as part of the overall analysis. This article provides a sensitivity analysis that is one component of that uncertainty analysis.
Introduction
Consider the standard leveling configuration that is used in power calibration as represented in the following image
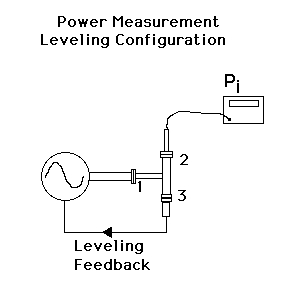
For this configuration the purpose of the leveling loop is to keep the available power constant regardless of the load placed on port 2. This has the effect of fixing the active source reflection coefficient. This reflection coefficient can be computed from the S-parameters of the power splitter using
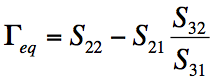
Typically the S-parameter uncertainties are expressed in terms of magnitude and phase. So the first step in a sensitivity analysis that would be part of an overall uncertainty analysis is to express the above equation in terms of the magnitude and phase. We will do this by defining sij=|Sij|, and defining the phase θij=Arg(Sij) resulting in
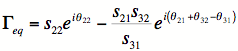
or
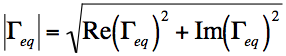
The magnitude of this quantity is
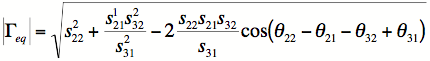
the real and imaginary parts of this are
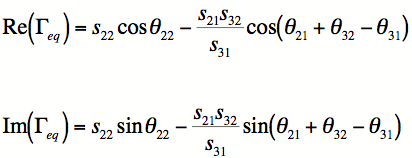
and the phase of this quantity is
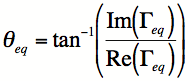
The uncertainty associated with the measured S-parameters magnitude will be denoted δsij, and the uncertainty in phase δθij.
Real and Imaginary Parts
Using standard sensitiviy analysis techniques, one would estimate the RSS uncertainty in the real and imaginary parts of Γeq using
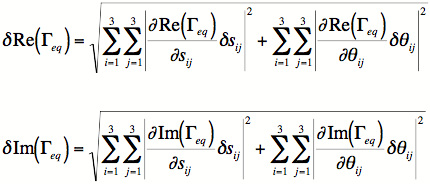
To complete the analysis of the uncertainty in the real and imaginary parts one need only enumerate the partial derivatives, which results in

Magnitude and Phase Uncertainty
Once the real and imaginary part uncertainties are determined, the magnitude and phase uncertainties associated with that are fairly easy to determin. The result for magnitude is

and for phase is
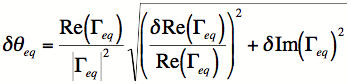
Note that in these equations all phase and phase uncertainties are assumed to be expressed in radians.
Conclusion
Here an equivlant source reflection coefficient uncertainty estimate has been presented that can be part of an overall uncertainty analysis of a power measurement system. It assumes that one has one has made S-parameter measurements of a power splitter and has determined the uncertainty associated with those parameters. This in itself may not be a trivial task. Please feel free to comment on this article in the forums.
Related LearningMeasure.com Courses
- UNC210 - Uncertainty Analysis of Complex-Valued Measurands
- EE104 - Introduction to RF/Mircrowave Concepts
- MEAS401 - Basic RF and Microwave Power Measurement

